2013-04-12-Graphs
Table of Contents
1 Graphs & Networks
1.1 Midterm Stats notes
- min 53.00
- max 87.00
- avg 75.53
- med 77.00
- stdev 9.28
2 Graphs
- Can model a surprising number of domains
- Modeling with network opens up large number of algorithms
- Linear math has many connection to graphs
2.1 Math notes
- Data mining theme: get your problem stated as a math problem, whole slew of solutions present themselves
- Linear math really useful for running equations of all nodes, are simulate moving across network
3 Vertices & Edges two_col
- Vertex
- the interconnected objects, or nodes
- Edge
- the lines or curves that connect vertices
- Graph
- Collection of vertices and edges
G = (V,E)
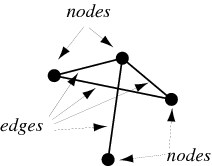
3.1 Definitions notes
- These are the abstract terms, how do they relate to the real world?
4 Examples
- Vertex
- User, building, router, product
- Edge
- Relationship, road, network cable, purchased
- Graph
- Social Network, physical infrastructure, internet, purchasing history
4.1 Examples notes
- Many graphs have assumed edge labels: they edges represent something consistent
- Some graphs have multiple times of edges: relationship is one of family, friend, co-worker, etc.
- Edge can be anything that ties two things together: purchase history, eg. is not a physical thing connecting, but an idea
5 Social Networks two_col
- Edge connecting two people
- If this is just a line, what information are we missing about how the link was formed?

5.1 Symmetric notes
- "Just a line" is symmetric, ie "undirected"
- We're missing information about who invited whom. Asymmetric and directed
6 Definitions two_col
- Directed
- Connections have a direction. Invitations, water pipes, email
- Undirected
- Connections have no direction. "Friends," walkways on campus, physical wires
- Cycle
- Set of nodes and edges in which you can travel back to a vertex
- Acyclic
- A graph without any cycles
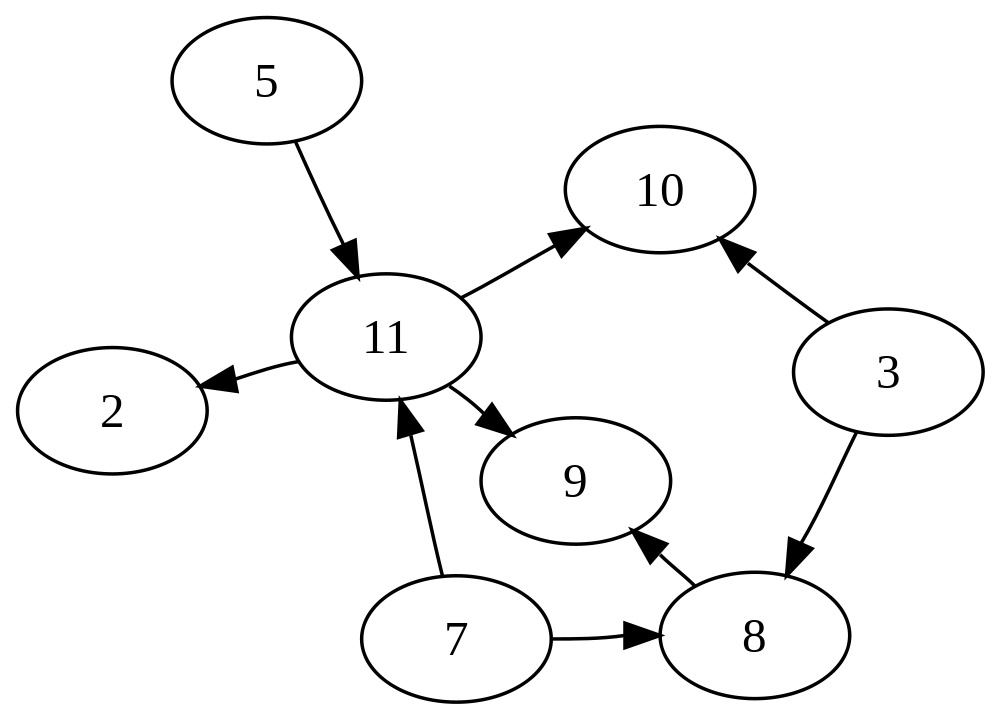
6.1 Modeling notes
- Can always model undirected graph as a directed one by having two connections between nodes always
7 Acyclic?
- Social network (undirected)
- Product purchases (directed)
- Internet links (directed)
- Class prerequisites (directed)
7.1 Answers notes
- Social network: cyclic
- Product purchases: acyclic
- Internet links: cyclic
- Class prerequisites: acyclic
8 Bipartite two_col
- Graph whose vertices can be divided into two distinct sets
- Vertices in
Uare only connected to those inV, vice versa - Product purchases: users
U, productsV
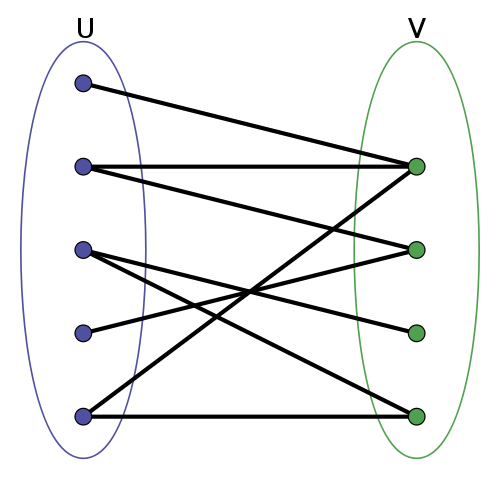
8.1 Recommendations notes
- Can model recommendations as link following:
- From a user, follow to products
- From products, follow back to other users
- From other users, follow back to products
9 Measurements
- Geodesic distance
- Number of edges to connect to vertices
- Eccentricity
- Largest geodesic distance from
vto another - Radius
- Minimum eccentricity
- Diameter
- Maximum eccentricity
- Peripheral vertex
- Vertex with eccentricity == diameter
- Incoming/Outgoing edge count
- Number of edges point to or from an edge
9.1 Data Stats notes
- Similar to getting distribution stats from initial datasets, these measurements can help you understand graphs as a summary
- Once you have the incoming/outgoing edge counts, can use regular stats: what is the distribution of counts?
9.2 Examples center
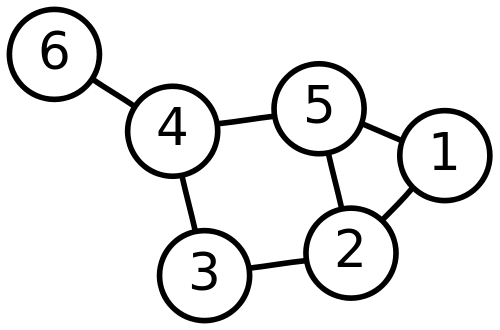
9.2.1 Answers notes
- Distance 6, 5: 2
- Eccentricity 2: 3 (disconnected graph is infinity)
- Radius: 2
- Diameter: 3
- Pericheral Verticies: 1, 2, 6
10 SimRank
- Vertices are similar if they share similar neighbors
- SimRank between two vertices is the average of the SimRank of its neighbors
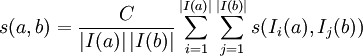
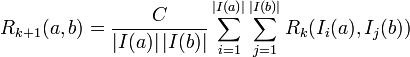
10.1 Recursive notes
- This is an iterative and recursive definition
- Iterative because neighbors are influenced by each other
- What is your simrank? Well, what is your simrank?
- Converges
- Recursive because you're figuring out simrank for all neighbors
10.2 Example

2 SimRank 4
10.2.1 Calculations notes
- I(u) = 5,3,1
- I(v) = 5,3,6
- C = 0.6 daming factor.. similarity fades over time
- s0(5,5) = 1
- s0(3,3) = 1
- s0(5,3) = 0
- s0(3,5) = 0
- s0(1,5) = s0(1,3) = 0, s0(6,1)… = 0
- s1= 0.6/(2*2) * sum(1,1,0,0,0,0)
- 0.3
- Next round, we'll need to figure out s1 of 5,3 to calculate update
11 Random Walk
- Many algorithms based on concept of randomly deciding:
- Follow link or not
- Which link to follow
- Simulate the decision many times
- What is the probability you will wind up on
ufromv?